This one was suggested by my friend Xavier :grinning:

He asked me if I could find where to cut a circular waffle along its diameter so that the total area gets divided into four equal parts. We set ourselves to work and we found that the answer was not as easy as we would have guessed.

We can inject some numbers into the problem by drawing a Cartesian system of coordinates with its origin at the centre of the waffle.

We will have solved the problem if we can find the value of the angle $\theta_0$ for which the area of the quarter circle above the red line is equal to the area below. This latter area can be obtained as the sum of the right triangle between the red and black lines in the figure plus another contribution which can be computed as an integral. Taking the radius of the waffle as the unit of length and using the polar coordinates, this integral reads

$$
\int_0^{\theta_0}\left(\int_0^1 r dr\right) d\theta=\frac{\theta_0}{2}~.
$$

Once we have added the area for the right triangle, we obtain the following constraint on $\theta_0$ :

$$
\frac{\theta _0}{2}+\frac{1}{2} \sin \left(\theta _0\right) \cos \left(\theta _0\right)=\frac{\pi }{8}~.
$$

Now, the solution to the original problem is equal to $\sin(\theta_0)$ where $\theta_0$ satisfies the above equation. This last step, however, cannot be done analytically.

We have here an example of an analytical function that is defined implicitly via its inverse. What it means is that, if you call the left-hand side of the above $f(x)$, then the inverse function, $f^{-1}(x)$, though analytical, has no closed symbolic form. The best we can do is to provide a numerical solution. This amounts to find the abscissa of the red dot on the graph below, which marks the intersections between each side of the above equation.

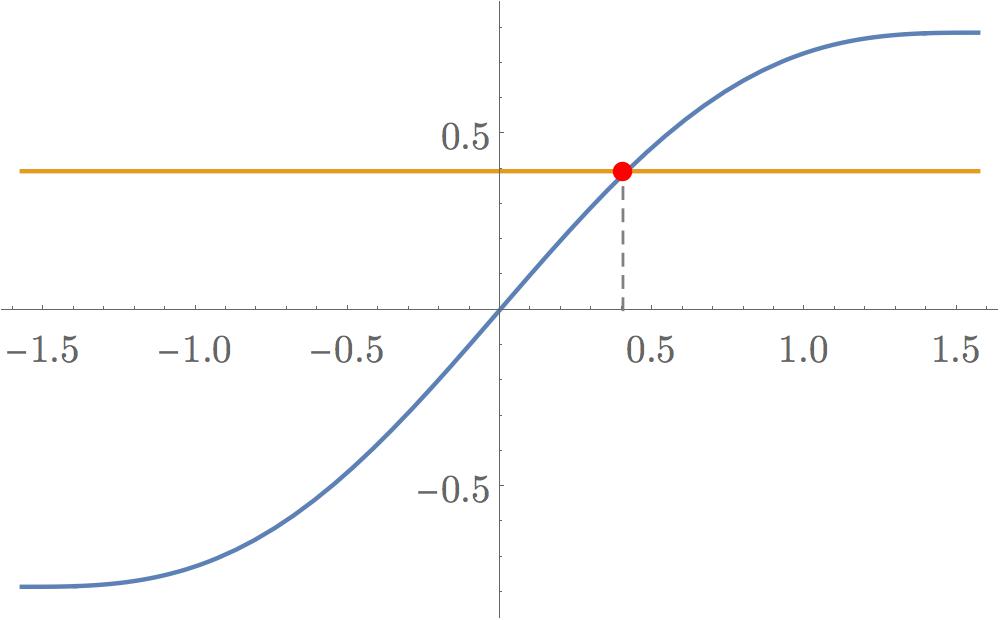
The end result is approximately :

$$
\theta_0=0.415856~~~\text{so that,}~~
\sin(\theta_0)=0.403973~.
$$