Everyone has heard the sound of a ball bouncing off the floor after being dropped from a certain height. This makes a distinctive thud—thud—thud-thu-th-tt-tt-t-… with the sound of every rebound coming closer to the next in time. This is due to the fact that the ball loses some of its energy at each rebound. In this post, I give a very simplistic model for this and hopefully learn something along the way.

Let's assume that the ball loses a fraction $\alpha$ of its energy everytime it touches the ground. We neglect the dragging force of the wind when the ball is in the air. The ratio of the energy between rebound $n$ and $n-1$ is then

$$\frac{E_n}{E_{n-1}}=(1-\alpha)~.$$

How can we measure the dissipation parameter, $\alpha$ ?

After it has bounced, the ball reaches some maximum height at which it comes to rest and so all its energy is contained in its (gravitational) potential energy. The ratio of height between two rebounds can therefore be guessed to be

$$\frac{h_n}{h_{n-1}}=(1-\alpha)~.$$

Now, it is quite impractical to measure the height of the ball before and after a given rebound. It is much easier to measure time intervals. From elementary kinematic, we know that the ball will drop from height $h_n$ in a time

$$t=\sqrt{\frac{2 h_n}{g}}~,$$

with $g$ being the gravitational acceleration. The ball makes a return trip from the ground up to its maximum height and back to the ground after it has bounced. The total time spent in the air between the rebound $n$ and $n+1$ is therefore:

$$t_n=2\sqrt{\frac{2h_n}{g}}~.$$

The ratio of two such consecutive time intervals is then

$$\frac{t_n}{t_{n-1}}=(1-\alpha)^{\frac{1}{2}}~.$$

It is interesting to see that, in our toy model, the ratio between any two succesive time interval is constant.

How long will it take for the ball to come to rest ? And after how many rebounds ? The answer to the first question is fairly easy to give but the answer to the second one may surprise some.

For the sake of simplicity, we further assume that the ball instantly transfer its energy to the ground as it bounces back, which is of course an idealisation. The total time spent in the air if the ball is initially dropped from an height $h_0$ and after $N$ rebounds is

$$T=t_0+\sum_{n=1}^Nt_n~,$$

where $t_0$ denotes the time for the initial drop and $t_n$ represents the time in the air after the $n^\text{th}$ rebound. Since we know the ratio of time interval between consecutive rebounds we may write:

$$T=t_0+t_1\sum_{n=1}^N(1-\alpha)^{\frac{n-1}{2}}~,$$

$$T=\sqrt{\frac{2h_0}{g}}+2\sqrt{\frac{2h_0}{g}}\sum_{n=1}^N(1-\alpha)^{\frac{n}{2}}~.$$

The series can be summed (as a geometrical progression) to obtain

$$T=\sqrt{\frac{2h_0}{g}}+2\sqrt{\frac{2h_0}{g}}\frac{(1-\alpha)^{1/2}-(1-\alpha)^{(N+1)/2}}{1-(1-\alpha)^{1/2}}~.$$

What is interesting about this expression, is that it converges to a finite number for $N\rightarrow+\infty$. We can take $\sqrt{\frac{2h_0}{g}}$ as the unit of time for simplification. The above expression therefore converges to

$$T=\frac{1+\sqrt{1+\alpha}}{1-\sqrt{1+\alpha}}~.$$

This quantity can be easily measured and so we can derive the value of $\alpha$ by solving the above:

$$\alpha=\frac{4T}{(1+T)^2}~.$$

The two above formula are represented in the graph below :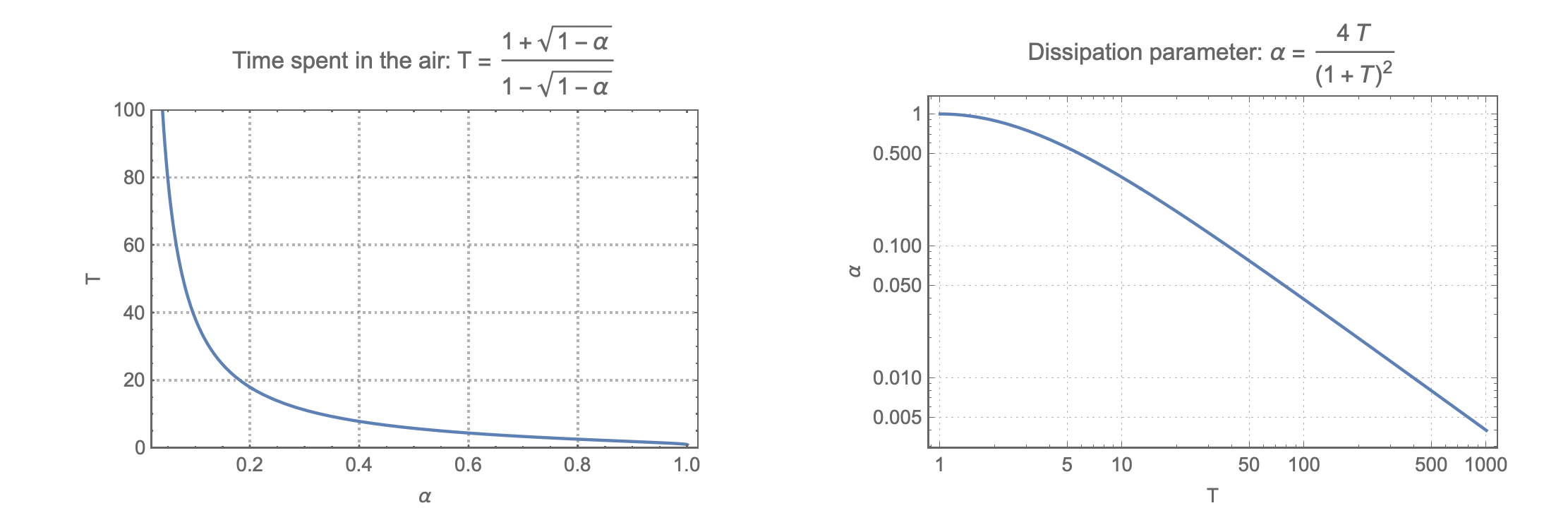

But hang on... In deriving the above, we have made the assumption that the number of rebounds goes to infinity $N\rightarrow+\infty$ yet the total time $T$ remains finite. Does the ball actually performs an infinite number of rebounds? And how is it possible for it to do so in a finite amount of time?

Well, first of all, one must not forget that we are dealing here with a very simplified toy model. In reality, there are a number of complications arrising. For example, the amount of energy dissipated at each rebound likely depends on the velocity of the ball as it hits the ground, etc...

Nevertheless, there is no contradiction in having an infinite number of rebounds happening in a finite time. The paradox exists only in appearance and can be traced back to a classic formulation known as the Zeno paradox. In short, the paradox is solved by realising that, after each rebound, the amount of time that the ball spends in the air decreases. In other words, it goes to zero when $n$ increases. At the end of the day, the two limits balance each other and the total time remains finite.