When you are stading on a beach, you can sometimes see ships disappearing behind the horizon. If we could measure the distance at which the ship completely disappears from our line of sight, we could infer the radius of the Earth. In this post, I want to do the opposite and infer the distance to the horizon based on our knowledge of the Earth radius. I had this idea while on holiday in Melbourne with my friend Jojo and we worked out the following computation together :)

I we make the approximation that the Earth is perfectly spherical, the situation looks like the following picture:

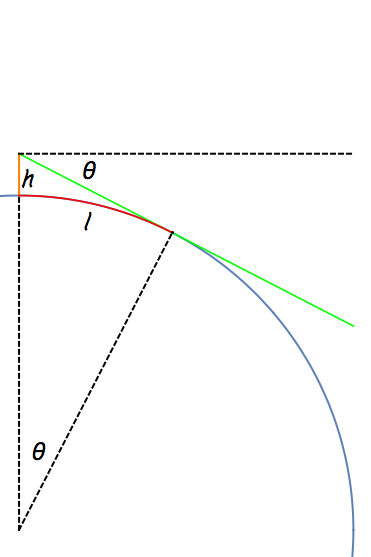
The distance that we are looking for is the red piece of arc labeled $l$. The problem will be solved once we have found the angle, $\theta$. Placing the origin of coordinates at the centre of the Earth and chosing its radius as our unit of length, we can derive the following equation for the line of sight (green line) :

$$
y = 1 + h -x\tan{\theta}~.
$$

Furthermore, the coordinates of all points on the circle must satisfy $(x,y)=(\sin{\theta},\cos{\theta})$, so finding $\theta$ is just a matter of solving

$$
\cos{\theta} = \frac{1}{1+h}~.
$$

I am $\sim180$cm tall ($\sim 6$ft), plugging this in the above gives a distacne of $4.8$km (about 3mi) to the horizon. One important question is to know how this results scales with the height of the observer. We can work this out by expanding the above equation in series of $h$.

$$
\theta\sim \sqrt{2}\sqrt{h}+\mathcal{O}[h]^{3/2}~.
$$

Interestingly, and to first order, this corresponds exactly to the answer obtained by assuming that $l$ is a straight line and using Pythagora's theorem. Our result has the advantage to remain valid at all order in $h$.