Rossby modes

The (linearized) momentum equation governing the dynamics of a fluid at a surface of the sphere with radius reads, in the spherical components:

where is the angular velocity of the reference frame (attached to the planet) and is the reduced pressure. In these coordinates and assuming that the motion is 2-dimensional, the condition of incompressibility , translates to:

Looking for oscillatory solutions with time-dependence proportional to , we may cast the above system in a single autonomous equation:

which may be rewritten as:

where and denote the toroidal components of the velocity. Equation corresponds to the general Legendre equation whose solutions are:

provided that the frequency satisfies the following dispersion relation:

These solutions are called Rossby modes. The first few of these are plotted here below on the Earth’s surface. From top to bottom: and from left to write: . Colors represent the radial vorticity.

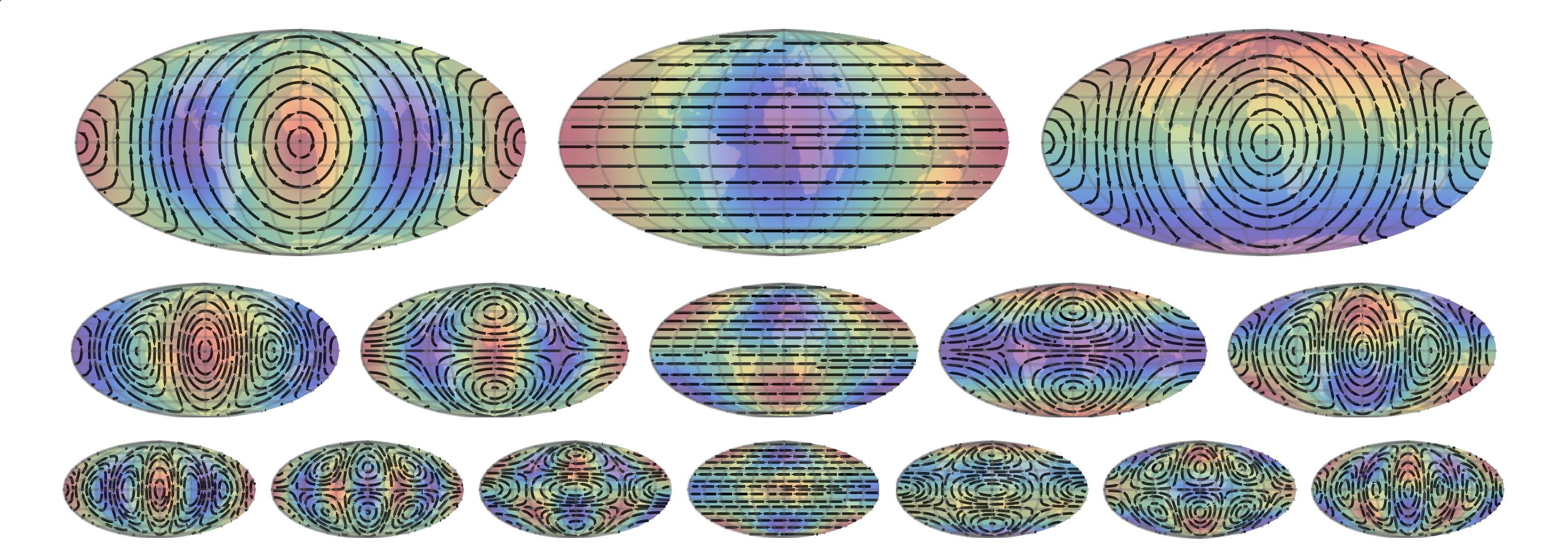
References

• Longuet-Higgins, M. S. Planetary waves on a rotating sphere. II (1965) ,Proc. R. Soc. Ser. A,284, 40
• Zaqarashvili et al. Rossby Waves in Astrophysics (2021)