February 13, 2022

jerem.
The (linearized) momentum equation governing the dynamics of a fluid at a surface of the sphere with radius $R$ reads, in the spherical components:
$$
\begin{align}
\partial_tu^\theta-2\Omega\cos\theta u^\varphi &=-\frac{1}{R}\frac{\partial p}{\partial\theta}~,\\
\partial_tu^\varphi+2\Omega\cos\theta u^\theta &=-\frac{1}{R\sin\theta}\frac{\partial p}{\partial\varphi}~,
\end{align}
$$
where $\Omega$ is the angular velocity of the reference frame (attached to the planet) and $p$ is the reduced pressure. In these coordinates and assuming that the motion is 2-dimensional, the condition of incompressibility $\mathbf{\nabla}\cdot\mathbf{u}=0$, translates to:
$$
\begin{equation}
\frac{\partial}{\partial\theta}\left(\sin\theta u^\theta\right)+\frac{\partial u^\varphi}{\partial\varphi}=0~.
\end{equation}
$$
Looking for oscillatory solutions with time-dependence proportional to $\sim\mathrm{e}^{i\left(\omega t-m \varphi\right)}$, we may cast the above system in a single autonomous equation:
$$
\begin{equation}
\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial}{\partial\theta}\left(\sin\theta u^\theta\right)\right)-m^2 u^\theta-\frac{2m\Omega}{\omega}\sin^2\theta u^\theta=0~,
\end{equation}
$$
which may be rewritten as:
$$
\begin{equation}
\left(\frac{\partial}{\partial\mu}\left((1-\mu^2)\frac{\partial}{\partial\mu}\right)-\frac{m^2}{1-\mu^2}-\frac{2m\Omega}{\omega}\right)\tilde{u}^\theta=0~.
\label{eq:Rossbyeq}
\end{equation}
$$
where $\mu=\cos\theta$ and $\tilde{u}^\theta=\sin\theta u^\theta$ denote the toroidal components of the velocity.Equation $\eqref{eq:Rossbyeq}$ corresponds to the general Legendre equation whose solutions are:
$$
\begin{equation}
\tilde{u}^\theta=\mathrm{P}_\ell^m(\cos\theta)~,
\end{equation}
$$
provided that the frequency satisfies the following dispersion relation:
$$
\begin{equation}
\omega=-\frac{2m\Omega}{\ell(\ell+1)}~.
\end{equation}
$$
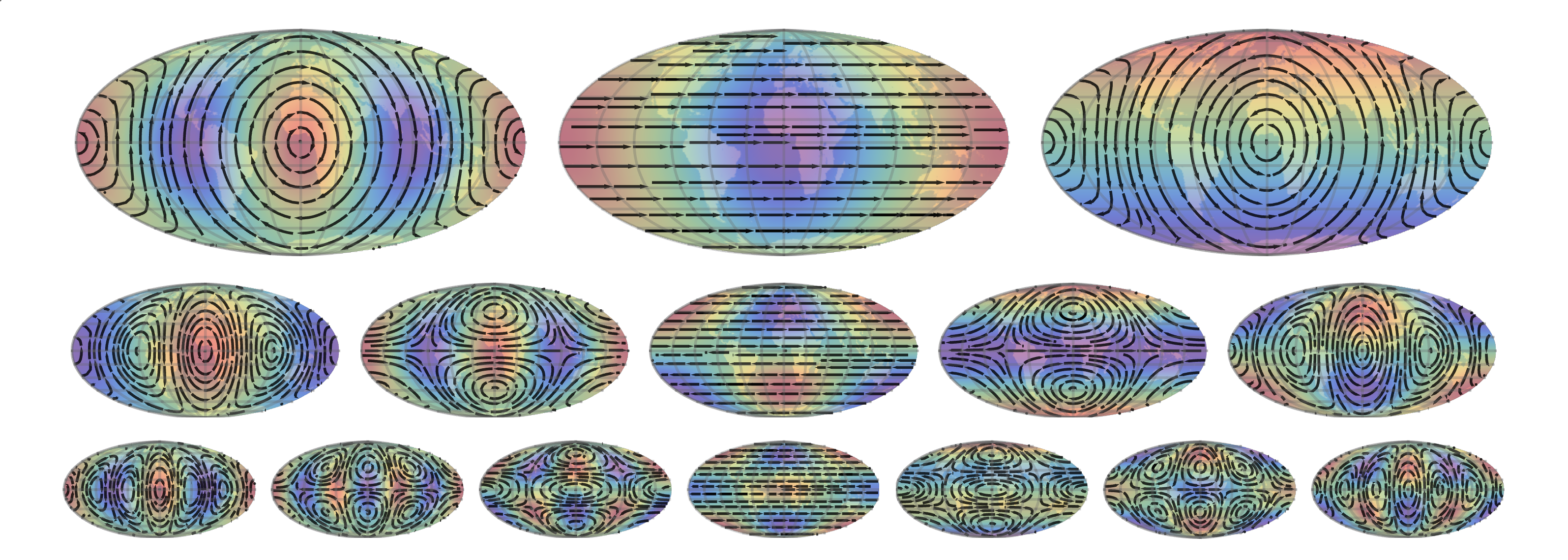
These solutions are called Rossby modes. The first few of these are plotted here below on the Earth's surface. From top to bottom: $1\leq\ell\leq3$ and from left to write: $-\ell\leq m\leq\ell$. Colors represent the radial vorticity.